PID 控制算法

Cortex-M4

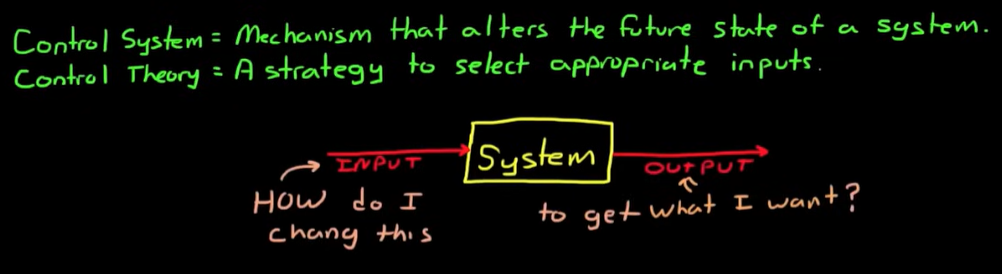
首先，对控制系统和控制理论的概念做简单的介绍。

学术点讲，控制系统就是能改变系统未来状态的一种装置，它独立于控制对象本身，是我们人为设计出来给控制对象以控制信号的装置；而控制理论就是帮助我们合理设计这种装置的方法和策略。

大白话讲就是，有一个系统（system），给它一个输入（Input），它就会有一个输出（output），现在我们想它按我们想的来输出。此时，控制系统就是产生输入的东西，控制理论则告诉我们到底给什么输入。

F407PIDkzsf

开环控制

开环控制指输入不依赖于输出的控制方式;

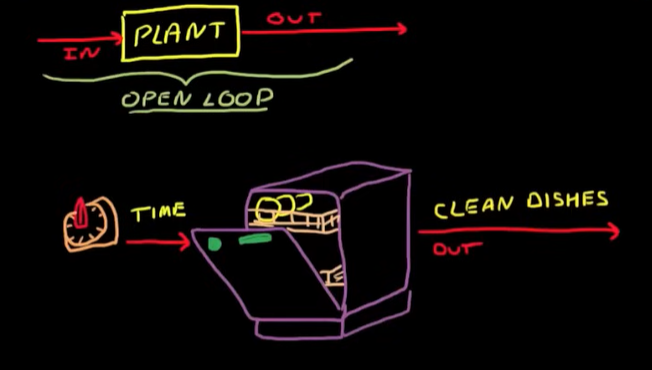
F407PIDkhkz

当我们只输入时间这个控制变量的时候，就是开环控制，因为控制量时间一经设置好就不变，不随着输出——盘子清洁程度的变化而变化;

对于一些精度不那么重要的系统来说开环控制非常友好

闭环控制

闭环控制指输出会反馈给输入端从而影响输入的控制方式;

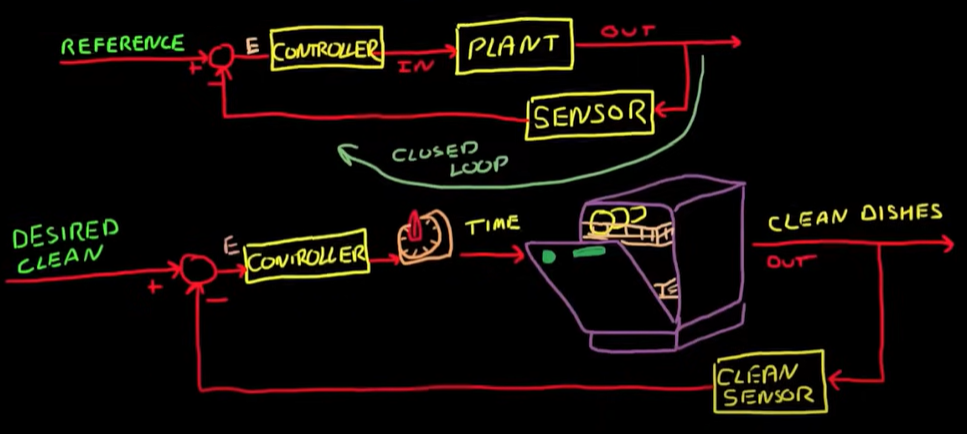
F407PIDbykz

闭环控制过程中，会首先设置一个参考值，这里即盘子的清洁程度；探测结果的会反馈到控制器的输入端，与我们设置的参考值进行比较，得到误差 E；控制器根据E得到输入出结果，如果E > 0，说明盘子还没洗干净，需要增加清洁时间 t，直到E = 0，盘子被清洗干净。这一不断反馈并修正输入的过程构成了完整的闭环，即“闭环控制”;

PID 控制算法

PID（Proportional-Integral-Derivative）控制算法是一种高效且简单的闭环控制算法，用于解决目标值与实际值的差异（误差）问题。

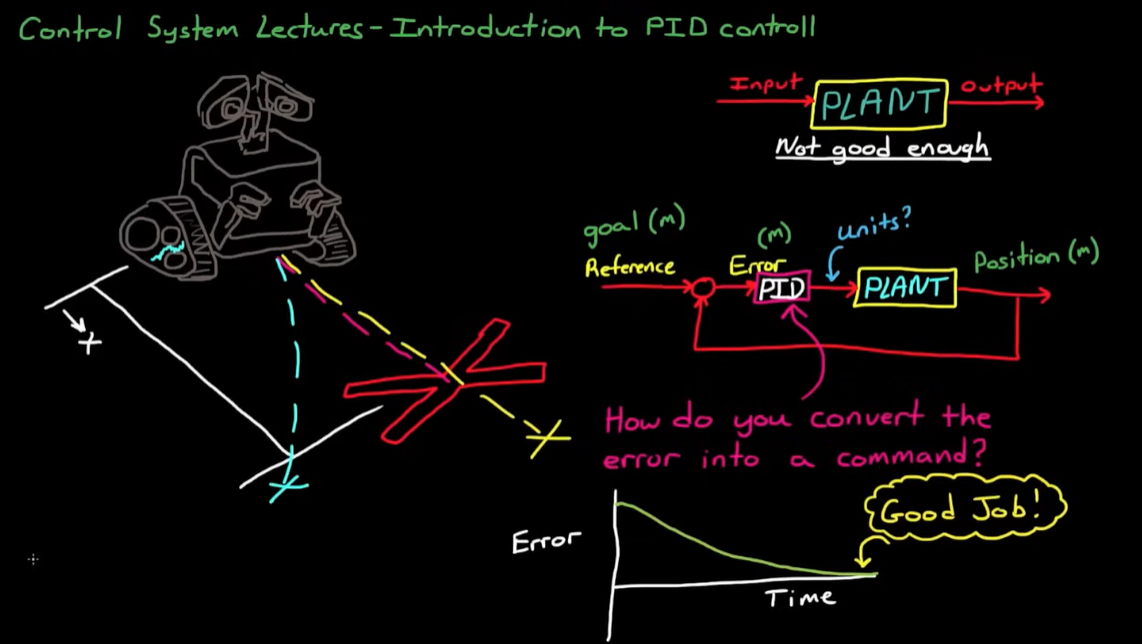
F407PIDshuom1

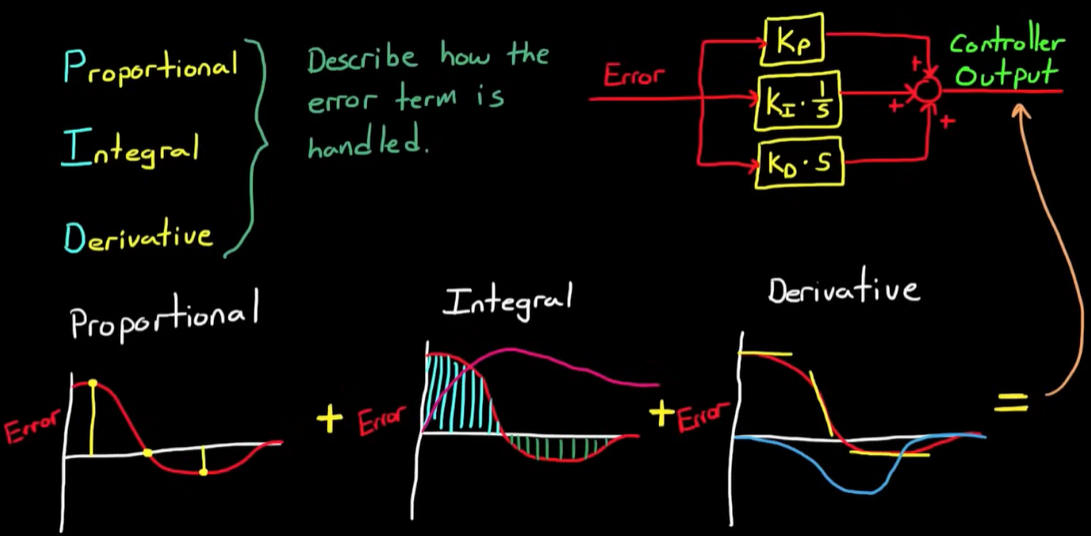
F407PIDshuom2

PID 代表：Proportional（比例），Integral（积分），Derivative（微分）。

输入的 误差 (Error) 被送入三部分：比例通道、积分通道和微分通道。

三个通道各自根据误差，贡献不同的控制量（用增益系数（误差）分别乘以 Kp、KI、KD 来调整每个通道的影响），然后相加形成最终的控制输出。

Proportional（比例）

基于当前误差的大小来做出调整。误差越大，控制器输出的调整越大。

Integral（积分）

根据误差随时间的累积来做出调整。积分控制的作用是消除稳态误差（当比例控制无法完全消除误差时，积分控制会通过不断累积误差来进行调整）。

理想状态下，通过 P 和 D 可以让小车停留在目标位置，但是实际情况是 P 在被 D 抵消的同时，重力、摩擦力等因素也会对小车产生影响，导致其永远达不到目标位置；

稳态误差

稳态误差 是控制系统在经过足够长的时间后，系统输出与目标值（期望值）之间的持续偏差。换句话说，当系统稳定后（即进入稳态时），如果输出值无法完全达到目标值，则这种残留的误差被称为稳态误差。

Derivative（微分）

据误差变化的速率来做出调整。它主要用于预测误差的变化趋势，并对系统的动态响应进行调整，抵消由 P 产生的震荡。

比例控制处理“当前误差”；

积分控制处理“过去误差”；

微分控制处理“误差变化趋势”。

简单来说，就是将误差进行比例放大，微分阻尼，积分误差补偿

PID分别是如何实现的？

比例控制（P）

1
2
3
4
// 计算出目标位置与当前位置的误差
double error = setpoint - measured_value;
// 比例 = 误差 * Kp，Kp 是我们指定的比例系数
double Proportional = error * Kp;
  • 比例控制的特点：它的优点是简单、快速，并且容易理解，但存在以下问题：
    1. 稳态误差：比例控制可能导致稳态误差（即即使控制系统在工作时，输出值也可能永远无法完全达到目标值）。这主要是因为比例控制始终是根据当前的误差做出调整，在误差减小时，控制输出也会减小，导致误差不能完全消除。
    2. 响应过快导致的震荡：比例控制可能会对某些系统造成过冲或震荡，尤其是在比例增益较大的情况下，系统过度调整，导致目标值的超调和再修正。

积分控制（I）

1
2
3
// 积分 i = i += 误差 * dt，
// dt 表示误差的采样间隔（采样时长）
double integral += error * dt;

如果系统长时间存在误差（即系统偏离目标值），积分项会不断累积这些误差，并逐渐加大控制输出，直到误差完全消除，从而让系统达到目标值。

微分控制（D）

1
2
3
4
5
6
// 微分 
double previous_error = 0.0; // 上一次的误差
// D 可以理解为速度 = 距离 / 时长
double derivative = (error - previous_error) / dt;
// 更新上一次的误差
previous_error = error;

D 可以理解为速度，当速度过快时（error - previous_error < 0），D 算法就会抵消一部分 P 算法计算出来的的动力，从而减缓系统的震荡；

求和

1
double output = Proportional + Ki * integral + Kd * derivative;

实现如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <stdio.h>

// 定义 PID 参数
// 这三个系数要通过调试来确定
double Kp = 1.0;  // 比例系数
double Ki = 0.1;  // 积分系数
double Kd = 0.01; // 微分系数

// 定义 PID 控制器变量
double previous_error = 0.0; // 上一次的误差
double integral = 0.0;       // 积分累积

// PID 控制函数
double pid_control(double setpoint, double measured_value, double dt) {
    // 计算误差
    double error = setpoint - measured_value;
    // 计算积分部分
    integral += error * dt;
    // 计算微分部分
    double derivative = (error - previous_error) / dt;
    // 计算控制输出
    double output = Kp * error + Ki * integral + Kd * derivative;
    // 更新上一次的误差
    previous_error = error;

    return output;
}

int main() {
    double setpoint = 10.0;  // 目标值
    double measured_value = 0.0; // 初始测量值
    double dt = 0.1;        // 时间步长（秒）

    for (int i = 0; i < 100; i++) { // 模拟 100 次迭代
        double output = pid_control(setpoint, measured_value, dt);
        measured_value += output * dt; // 模拟系统响应
        printf("Iteration %d: Output = %f, Measured Value = %f\n", i + 1, output, measured_value);
    }
    return 0;
}

位置式PID 和 增量式PID

位置式PID

位置式 PID 计算的是控制量的绝对值，即每个时刻控制输出是基于当前的误差值、误差的积分和微分来直接计算的，控制输出是绝对的目标位置。

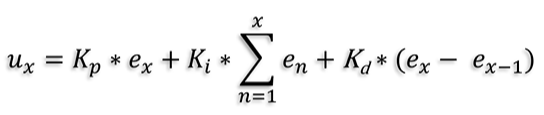
F407PIDweizhigongshi

增量式PID

增量式 PID 计算的是控制量的增量，即当前时刻的控制输出是与前一个时刻控制输出的变化量（增量）相关，而不是直接计算出控制输出的绝对值。增量式 PID 关注的是如何调整控制量（而不是绝对的目标值），因此每一时刻的输出量是基于上一时刻的输出和当前误差来调整的。

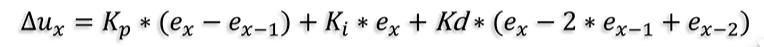
F407PIDzengliangshi

二者区别

特性 位置式 PID 增量式 PID
输出形式 直接计算控制量的绝对值 u(t)u(t)u(t) 计算控制量的增量 Δu(t)\Delta u(t)Δu(t)
计算方式 当前位置的控制输出由误差、积分和微分直接计算 当前的控制输出由上一时刻的控制输出和误差的变化量计算
使用目的 适用于需要计算绝对控制输出的系统 适用于需要计算控制增量，控制量依赖于之前的输出的系统
控制量变化 控制量的变化直接由误差决定 控制量的变化由误差的增量和历史误差决定
优点 简单直观，适合许多标准控制应用，输出计算清晰 控制器对系统响应的调节较为平稳，尤其是对于一些已知参考模型的系统
缺点 容易受到数值积累的影响，可能导致积分饱和等问题 对于初始误差较大的系统，可能需要更多的调整和调试